How many handshakes

Introduce the problem to students:

How many handshakes would there be if everyone in the classroom shook hands exactly once?

To begin, have students simplify the problem. That is, they work out how many handshakes there are in smaller groups such as 2, 3, 4, 5 or 6 people. They can then use various problem-solving strategies such as acting the problem out, drawing diagrams, making a results table, or writing a mathematical statement.

Pose questions such as:

• Can you explain what is happening in the shape diagrams?
• What patterns can you see in the table?
• Can we represent this using other materials?
• Does this situation remind you of other problems?

Use blocks to explain the actions performed by the group. This video demonstrates how to do this.

Geometric shapes can be used to help students reason. For example, students could work out that each person (n) has a total of n-1 handshakes (as they cannot shake hands with themselves). This can be drawn or made on a geoboard. Refer to one of the diagrams above eg the square diagram, but this time show all the possible handshakes with repeats. The circles represent people (4) and the lines show the number of handshakes each person would have (3), To find the total students will need to multiply, 4 × 3 = 12

Encourage students to analyse the arrows and explain what they see i.e. every handshake is doubled. Pose the question: how would we get rid of the doubles? Students will hopefully recognise that the opposite of doubling is halving and therefore divide their answer by 2.

To extend the problem have students write a generalisation to work out how many handshakes between larger groups of people. They can achieve this by analysing the table or using their justification above to write a mathematical sentence, i.e. in a group with n people, each person will have a total of n – 1 handshakes, considering we do not want to repeat handshakes we divide this number by 2 which gives the rule <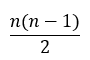.